Study Area
The study focused on all areas that were mapped as corn or soybean over the 10-year period from 2008 to 2017 in the contiguous US.
Database
Data sources* used in this analysis are listed below:
- Cropland data layer (CDL) - Annual raster-format land-use map created by the USDA-NASS.
- Historical state- and county-level corn yield data (USDA-NASS, 2008-2017).
- Enhanced Vegetation Index (EVI) images - 250 m resolution satellite images.
- Average temperature and growing degree units (GDU).
- Vapor pressure deficit (VPD) data.
- Soil data - Percent clay, available water content (AWC), organic matter content (OMC), and pH.
For each year considered in this study, the cropland data layer was re-projected to the MODIS sinusoidal projection and only pixels containing 100% corn or 100% soybean coverage were kept. All the information from the other raster layers (weather and soil) were extracted to the re-projected cropland data layers.
A 250-m resolution multi-band raster layer containing the following information was produced for each year of the study period: multitemporal EVI, accumulated precipitation, accumulated GDU, average temperature, average VPD, soil pH (0-30 cm), clay content (0-30 cm), available water capacity (0-30 cm) and organic matter content (0-30 cm). Since yield data were gathered at the county level, it was not possible merge that information on this raster layer.
Yield Forecast Model
An empirical relationship between USDA-NASS yield and multitemporal enhanced vegetation index was performed individually for each year at county level (EVI was averaged to county level).
Yield Prediction
Since the yield forecast model was trained in a coarse scale (county-level), yield was forecast using a 15-km grid layer rather than the MODIS native resolution (250 m). A 15-km scale avoided losing too much spatial information while the predictions were less affected by the difference of scale between the model training and application (related to 250 m), and it was helpful for further data manipulation, because it avoided problems with missing data in the temporal dimension (pixels were rarely tagged as corn or soybean in all ten out of ten years). All the analyses were performed using different scales (10 km, 15 km, 50km and county-level) to check the impact of the scale on the output.
The year-specific yield forecast models were applied on each one of the 15 km layers, and the predicted yield was normalized as relative yield.
relative yield = (yield - min yield)/(max yield - min yield)
Yield layers were geographically stacked and the average and the coefficient of variation were calculated for each cell over time. Only pixels tagged as crop in at least 4 out of 10 years were used.
Cluster Analyses
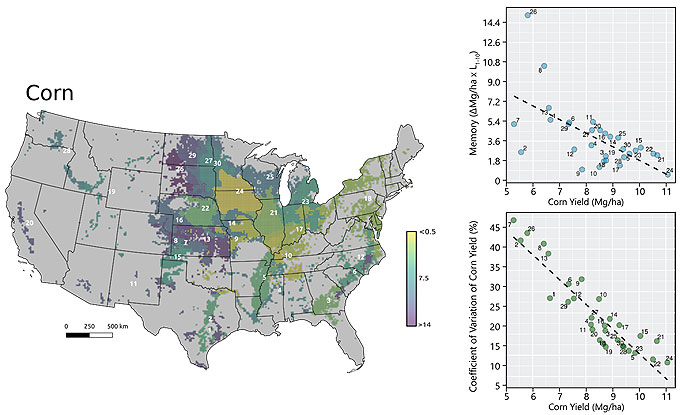
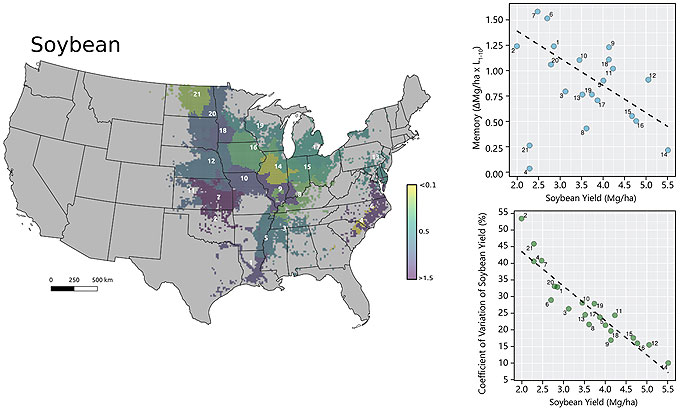
Cluster analyses were performed for each crop individually. Dissimilarity matrices with Euclidean distance were built for crop variables (average yield and CV) and for spatial variables (latitude and longitude). For the purposes of this study, the clusters are referred to as yield factor domains.
Within-Cluster Spatial and Temporal Stability
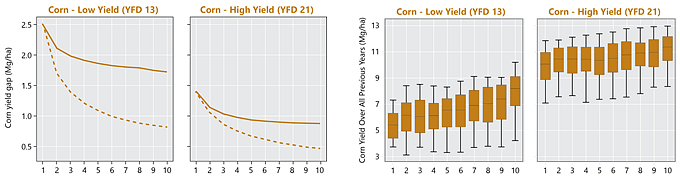
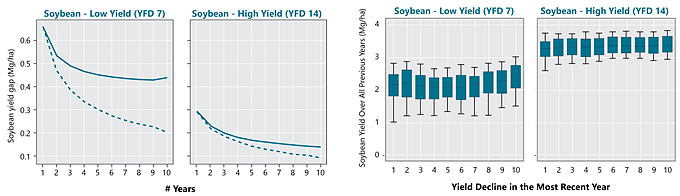
Contribution of persistent and non-persistent factors to yield gaps for corn and soybean were explored within each cluster. Yield gap (Yg) was assumed as the difference between the 95th percentile yield and average yields. For building the yield gap profile, yield gap was estimated for different length of years, denoted by L. The yield maps were averaged using all possible combinations for different length of the record (in # of seasons) and the Yg was estimated for L varying from 1 to 10. The steepness of the curve and the distance between lines provide insights into how persistent spatial yield differences are throughout the study period, and thus how important persistent factors like soil quality or farmer skill are in explaining the overall yield gap. The area between the two lines was calculated to numerically quantify the persistence of yield gap over the time within each cluster. This metric was termed yield memory (Figure 1).
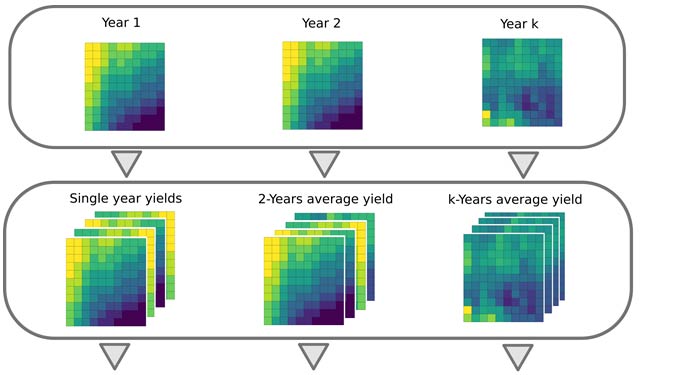
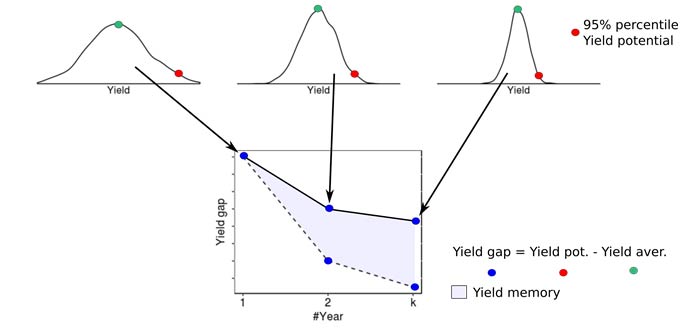
Figure 1. Summary of procedure to compute yield gap profiles and yield memory. Images from multiple years are averaged to create maps of average yields for varying periods of time. The maps are then used to compute the difference between maximum and average yields for the yield factor domains, and this difference is plotted versus the number of years used in the average (solid line). The dashed line portrays the expected change in yield gap with increasing years if yield patterns were entirely random in space. The shaded area between the lines represents the yield memory.
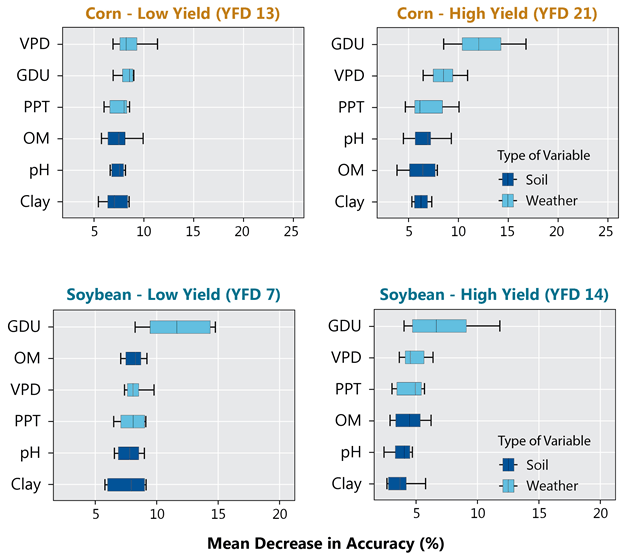
Within each cluster, a random forest algorithm with weather and soil variables as predictors was used to check the importance of each factor in explaining differences in yield. The importance of each weather and soil variable was computed from permuting the out-of-bag data (data that was not used for building the trees). For each tree, the prediction error of the out-of-bag portion of the data was recorded. Then the same was done after permuting each predictor variable. The difference between the two was then averaged over all trees and normalized by the standard deviation of the differences. The framework presented in Figure 2 summarizes the main steps of all analyses performed in this study.
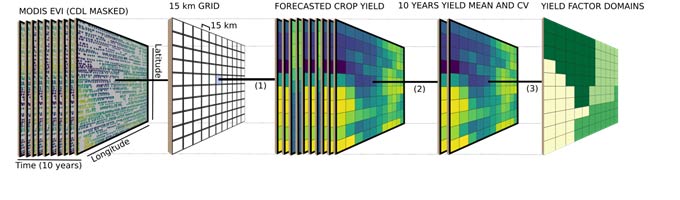
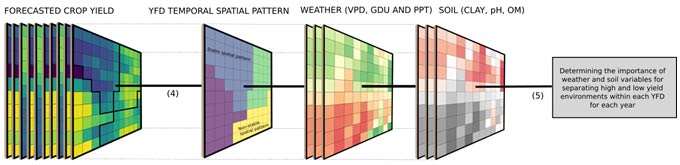
Figure 2. Analysis framework showing steps (1) crop yield forecast and data aggregation to 15 km, (2) data summarization (mean and coefficient and variation), (3) spatial constraint clustering, (4) estimate of the stability of the spatial pattern over years, and (5) evaluation of the influence of weather and soil attributes on the stability of spatial patterns.